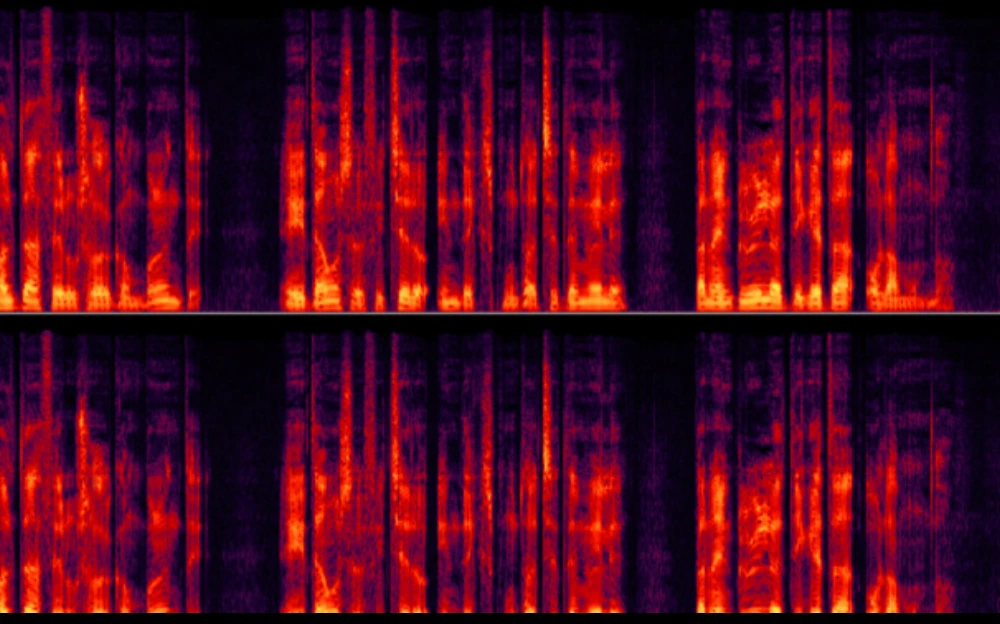
El fenómeno del ruido, representado matemáticamente como una función f(x) o f(t), puede ser desentrañado de manera fascinante mediante la transformada de Fourier. Esta herramienta matemática nos permite descomponer el ruido en una serie convergente de términos, donde cada uno de estos términos se corresponde con una componente frecuencial única de la señal.
La clave de este proceso radica en la capacidad de la transformada de Fourier para desglosar el ruido en sus elementos más fundamentales. Cada término de la serie resultante no es simplemente un número, sino más bien una ventana hacia una frecuencia específica presente en la señal de ruido. Es como descomponer una sinfonía caótica en sus notas individuales.
No menos importante es el papel de las constantes que acompañan a cada sumando. Estas constantes son las amplitudes, determinantes cruciales que indican la magnitud de cada componente frecuencial en la composición general del ruido. Así, la amplitud no solo cuantifica, sino que también revela la importancia relativa de cada frecuencia en el concierto del ruido.
Al explorar los espectros del ruido, no solo estamos descomponiendo un fenómeno aparentemente caótico, sino que también estamos revelando la riqueza oculta en su estructura. Este enfoque no solo tiene implicaciones en el ámbito matemático y científico, sino que también posee aplicaciones prácticas en campos como el control de ruido.
Comprender la transformada de Fourier y sus espectros asociados nos brinda la capacidad de intervenir y modificar selectivamente las frecuencias, permitiéndonos, por ejemplo, mejorar el confort acústico interno de un espacio. Así, al desvelar los secretos detrás de los espectros del ruido, abrimos la puerta a soluciones innovadoras y a una apreciación más profunda de un fenómeno omnipresente pero a menudo subestimado: el ruido.